Наша современная картина мира основана на двух теориях: Стандартной Модели физики элементарных частиц и Общей Теории Относительности, теории гравитации. Эти две теории отмечены удивительными успехами. Поэтому весьма поражает, что эта картина законов физики противоречива. Несогласованность происходит оттого, что одна часть теории, стандартная модель, рассматривается как квантовая теория, в то время как другая, гравитация, как классическая. На первый взгляд кажется, что все, что мы должны сделать - это проквантовать общую теорию относительности.

Перевод, уже ставшей классикой статьи Juan Maldacena. Gravity, particle physics and their unification

Популярную версию статьи этого же автора: Черные дыры и структура пространства-времени

Подборка статей по теории струн

Если использовать разложение в терминах фейнмановских диаграмм (методика, используемая в стандартной модели), то здесь возникают бесконечности, которые не могут быть поглощены перенормировкой константы Ньютона (и космологической постоянной). Фактически, при переходе к все более высоким порядкам теории возмущений необходимо включать все больше контрчленов.

Другими словами, теория неперенормируема. Так что принцип, который является столь критическим для построения Стандартной Модели дает сбой. Тем более удивительно, что непоследовательная теория может так хорошо согласовываться с экспериментом! Вот что происходит на самом деле: квантовые эффекты гравитации очень малы из-за слабости гравитации относительно других сил. Так как эффекты гравитации пропорциональны массе, или энергии частицы, они растут при высоких энергиях. При энергиях порядка $Е \sim 10^{19}Gev$ гравитация имела бы силу, сопоставимую с другими взаимодействиями Стандартной Модели (Это масштаб энергий, где мы определенно должны увидеть новую физику, однако возможно, что квантовая гравитация становится важной при энергии, которая намного ниже, $E \sim 1-10 Tev $).

Мы должны также помнить, что физика, насколько мы ее понимаем теперь, не может объяснить наиболее важный "эксперимент", который когда-либо предпринимался: Большой Взрыв. Весьма интересно, что теория Большого Взрыва связывает физику высоких энергий и космологию, и чтобы понять, что же произошло в самом начале, кажется, мы должны понять квантовую гравитацию.

Имеются также эстетические причины нашего желания иметь теорию, выходящую за пределы Стандартной Модели. Мы хотели бы объяснить происхождение калибровочной группы, соотношения между константами трех взаимодействий, остальную часть параметров стандартной модели, почему существует три поколения и т.д. Весьма наводит на размышления то, что когда вы экстраполируете поведение констант взаимодействий, они, по-видимому, совпадают при энергиях близких к тем, где становится важной квантовая гравитация, тем самым предполагая, что теория Великого Объединения, основанная на большей калибровочной группе, в любом случае лежит близко к планковскому масштабу.

Современная ситуация аналогична той ситуации в физике элементарных частиц, когда у нас имелась только теория слабых взаимодействий Ферми. Эта теория хорошо согласовалась с экспериментами, выполненными при низких энергиях, но она не была последовательной. Перенормируемость, или математическая самосогласованность, стала решающим ключом к открытию Стандартной Модели.

Проблемы, стоящие перед нами, могут быть разделены по степени трудности на следующие три группы:

Мы знаем, что есть теория, называемая теория струн (или М-теорией), которая уже способна обеспечить решение первых двух проблем. К сожалению мы все же не знаем, как решить третью. Возможно теория струн и является решением, мы только должны лучше ее понять, или может быть, ее требуется некоторым образом изменить. Теория струн - строящаяся теория. Мы знаем несколько ее пределов и аспектов, но мы все еще не знаем фундаментальных аксиом теории, которая дала бы нам возможность приблизиться к решению третьей проблемы.

Рис. 1: Фейимаиовские диаграммы для струн и частиц, (а) Свободное распространение частицы. (Ь) Вершина взаимодействия между частицами, (с) Свободно распространяющаяся струна, (d) Струна, взаимодействующая с другими струнами.

Рассеяние адронов в представлении фейнмановских диаграмм и теории струн.

Таким образом, если у нас имеется натянутая струна, ее колебание распространяется вдоль нее со скоростью света. Натяжение - размерная величина, которую мы можем параметризовывать в терминах масштаба длины: $T=1/l^2_s.$

Струны могут колебаться. Эти колебания могут быть разложены по нормальным модам. Так как струны - квантовомеханические объекты, каждой нормальной моде будет соответствовать некоторое число заполнения. Полная энергия колеблющейся струны будет проквантована. И полная масса колеблющейся струны будет равна полной энергии, содержащейся в ее колебаниях. Когда мы рассматриваем эту колеблющуюся струну издалека, она напоминает точечный объект. Различные возбужденные состояния струны аналогичны различным состояниям поляризации частиц, теперь масса состояния струны непосредственно зависит от состояния "поляризации".

Некоторые из возбужденных состояний струны будут иметь нулевую энергию и оказываются, таким образом, безмассовыми частицами. Имеется одно состояние со спином два, которое может рассматриваться как гравитон. Массы массивных состояний струны имеют порядок $m\geq 1/l_s.$ Мы вводим взаимодействия струны, позволяя струнам, которые касаются друг друга, соединяться в одну струну. Это будут взаимодействия разбиения и соединения, как показано на рисунке 1 (с, d). Амплитуда этого процесса определяет константу взаимодействия струн $g.$ Чтобы рассчитать любой процесс в теории струн, мы должны просуммировать по всем возможным взаимодействиям - разбиениям и соединениям. Самые простые теории струны - те, что живут в десяти измерениях и суперсимметричны. Суммы по фейнмановским диаграммам теории струн могут быть вычислены и дают конечные результаты. При низких энергиях, то есть, при энергиях ниже, чем массы массивных состояний струны $E\ll 1/l_s,$ единственными возбуждениями будут гравитоны и другие безмассовые частицы. Взаимодействия этих частиц описываются эйнштейновской гравитацией плюс некоторые другие безмассовые поля.

Таким образом, теория струн умеет квантовать гравитацию. То, что мы описали здесь, представляет собой квантование по теории возмущений, так же как разложение по фейнмановским диаграммам в физике элементарных частиц является квантованием по теории возмущений в теории поля. Но имеются и непертурбативные аспекты теории, которые не фиксированы теорией возмущений. Один из примеров - солитонные решения, подобные магнитным монополям теорий Великого Объединения. Это коллективные возбуждения, которые являются устойчивыми, как правило, благодаря некоторой топологической причине. Их массы ведут себя как $m \sim 1/g^2$ и в приближении слабого взаимодействия мы можем изучать их как экстремали классического действия теории поля. В теории поля нам также могут встретиться протяженные солитоны, подобные космическим струнам или границам доменов. В теории струн тоже существуют солитоны.

Эти солитоны называются D-бранами. D-браны - это солитоны различных размерностей. Они могут быть точечными (D-0-браны), одномерными (D-1-браны), двумерными (D-2-браны) и т.д. Эти солитоны очень точно описываются теорией струн [10]. Их возбуждения описываются открытыми струнами, которые на них оканчиваются. При низких энергиях некоторые из открытых мод струны безмассовы, имеют единичный спин и порождают калибровочные поля. Когда мы помещаем много бран вместе, открытые струны имеют два индекса $i, j$ маркирующие брану, где они начинаются и брану, где они оканчиваются, (см. Рисунок 2). Эти два индекса становятся индексами неабелевых $U(N)$ калибровочных полей.

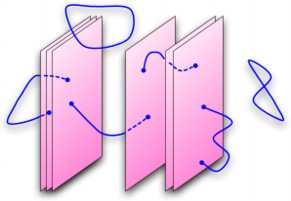
Рис. 2: D-браиы - протяженные солитоны, чьи возбуждения описываются открытыми струнами, которые заканчиваются на бране. Струна, идущая от браны i к бране j помечена двумя индексами. Они порождают неабелевы калибровочные поля, живущие на D-бране.

Может показаться удивительным то, что мы обсуждали десятимерную теорию, в то время как наш мир "очевидно" четырехмерен. Что мы в действительности видим - это то, что мир является четырехмерным на больших расстояниях, на самом деле, мы не знаем размерности мира на достаточно малых расстояниях. В теории струн мы предполагаем, что живем в мире, который имеет четыре больших измерения (те, что мы видим) и шесть очень маленьких измерений, см. Рисунок 3. Есть хорошо известное явление в физике твердого тела: если электрон заключен на очень узком энергетическом уровне, он ведет себя так, как будто перемещается только в двух измерениях. Подобным образом, частицы, которые двигаются в десятимерном пространстве с шестью маленькими измерениями, будут вести себя при низких энергиях так, как если бы они перемещались только в четырех измерениях.

Рис. 3: Изображение десятимерной геометрии вида $R^4 \times M^6$, где $M^6$ - малое шестимерное пространство, a $R^4$ представляет четыре больших измерения, которые мы видим: 3 пространственных и временное.

Каков размер этих дополнительных размерностей? Традиционное представление говорит, что они являются весьма маленькими, порядка $10^{-33} cm.$ Но недавно было понято, что некоторые измерения могли бы достигать размеров $1 mm $ [9]. В этом случае все поля стандартной модели должны быть заключены на D-бране, которая простирается вдоль четырех протяженных измерений, видимых нами, но поперечна большим дополнительным размерностям. Выбирая различные многообразия или различные бранные конфигурации мы можем при низких энергиях получать различные частицы.

В обоих случаях параметры стандартной модели зависят от деталей строения внутреннего многообразия или бранной конфигурации. Компактификации, сохраняющие 8,4 или 2 суперсимметрии при низких энергиях, поняты довольно хорошо. Случай, когда мы сохраняем только одну суперсимметрию, еще не изучен так же хорошо, и мы не понимаем, как можно нарушить суперсимметрию, в той степени, как это имеет место в реальном мире, избежав при этом возникновения огромной космологической константы, имеющей порядок масштаба нарушения суперсимметрии. Это, кажется, наиболее важное препятствие на пути точного понимания того, как же Стандартная Модель вложена в теорию струн.

Недавнее продвижение в теории струн было основано на идее дуальностей. Известно, что классический электромагнетизм инвариантен при взаимной замене электрических и магнитных полей $\vec{E}\to \vec{B},\vec{B}\to -\vec{E}.$ При этом обмениваются ролями электрические заряды с магнитными. В теории поля элементарные частицы несут электрические заряды, а солитоны - магнитные заряды. Так что эта дуальность меняет местами элементарные частицы с солитонами. Это может быть достигнуто путем замены константы взаимодействия $g\to 1/g$ так, чтобы солитоны, которые были тяжелыми, стали легкими, подобно элементарным частицам. Во многих теориях струн имеются дуальности этого типа. Когда взаимодействие в терминах некоторых переменных становится сильным, теория имеет эквивалентное описание на языке некоторых двойственных переменных, которые могут быть слабо взаимодействующими. Таким образом взаимосвязаны многие теории струн. Эти дуальности трудно проверить, так как требуется точно решить сильновзаимодействующую теорию, чтобы показать, что она - та же самая как и некоторая дуальная слабовзаимодействуюгцая теория. В суперсимметричных случаях имеется несколько величин, которые можно вычислить точно и которые не зависят от силы взаимодействия.

Они могут быть рассчитаны при слабом взаимодействии, проэкстраполированы к сильному взаимодействию и затем сравнены с соответствующим результатом дуальной теории. По этой причине, дуальности были проверены главным образом в суперсимметричных теориях. Вот примеры величин, которые защищены суперсимметрией и могут быть сосчитаны: 1) низкоэнергетическое эффективное действие, 2) число и массы различных "защищенных" специальных состояний, обычно являющихся заряженными частицами. Эти состояния могут быть элементарными в одной теории и солитонами в дуальной теории. Книги по теории струн: [1, 2]

Перевод осуществил В.О. Соловьев.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.