Один из наиболее загадочных результатов космологических наблюдений последнего времени состоит в том, что около 90% массы Вселенной состоит не из барионов и электронов, а из некоторой неизвестной субстанции, не испускающей и не поглощающей электромагнитные волны. По этой причине субстанция получила название «темная материя». В обзоре подводится итог теоретического и наблюдательного изучения темной материи. Кратко рассмотрены частицы-кандидаты на роль темной материи и обсуждены возможные стратегии ее детектирования. Мы показываем, что слабо взаимодействующие массивные частицы с массой порядка 100 ГэВ естественно воспроизводят наблюдаемую реликтовую плотность темной материи. Особо подчеркивается, что для решения проблемы темной материи и связанных вопросов  требуется информация, полученная как в рамках теории элементарных частиц, так и непосредственно космологии. В частности, рассматривается полезность космологических наблюдений для подтверждения суперсимметрии и наоборот

Мы хорошо знаем, из чего сделана наша планета, другие планеты солнечной системы и само Солнце. Их основными структурными составляющими являются барионы – сильно взаимодействующие частицы (адроны) с полуцелым спином. Небарионная материя, в которую до недавнего времени включали фотоны и нейтрино, казалось бы, не могла давать существенного вклада в общую массу Вселенной, так как масса фотонов равна нулю, а масса нейтрино, хотя и неизвестна, но, скорее всего, очень мала. Такое представление претерпело за последнее время существенное изменение. Помимо простого любопытства, из чего устроена Вселенная, в которой мы живем (им можно было и ограничиться в случае стационарной Вселенной), материальное содержание Вселенной играет важнейшую роль, так как определяет динамику Вселенной, а значит и ее конечную судьбу. Остановимся подробнее на последнем утверждении.
Динамика Вселенной описывается уравнениями Эйнштейна, которые, вообще говоря, являются сложными нелинейными уравнениями [1]:

Тензор энергии-импульса ${T_{\mu \nu }}$- описывает распределение масс в пространстве, а компоненты тензора кривизны ${R_{\mu \nu }}$ и его шпур $R$ выражаются через метрический тензор${g_{\mu \nu }}$ и его первые и вторые производные, $G$-гравитационная постоянная. Смысл этих уравнений крайне прост: геометрия (левая часть (1)) диктует массам (правая часть (1)), как двигаться, а массы диктуют пространству, как изгибаться. Несмотря на простоту физического смысла, нахождение общего решения такой сложной системы уравнений, как полевые уравнения Эйнштейна, безнадежная задача. Проблема упрощается при рассмотрении распределения масс со специальными свойствами симметрии. Основное предположение, лежащее в основе подавляющего большинства космологических моделей, пространственная однородность и изотропность. Наиболее общая пространственно-временная метрика, согласующаяся с этими симметриями – метрика Friedmann-Robertson-Walker (FRW):

где $a(t)$- так называемый масштабный фактор. Рассмотрим две точки, находящиеся в данный момент времени на расстоянии ${\vec r_0}$, не испытывающие действия никаких внешних сил и не участвующие ни в каком другом движении, кроме общего расширения Вселенной. Тогда физическое расстояние между этими точками$\vec r(t)$будет увеличиваться со временем как $\vec r(t) = a(t){\vec r_0}(t)$. Динамика масштабного фактора – основной объект исследования: в некотором узком смысле основная задача космологии и есть нахождение зависимости $a(t)$.
Если масштабный фактор содержит всю динамику Вселенной, то величина $d{l^2}$ описывает геометрию пространства

которое может быть либо плоским евклидовым, если кривизна $k = 0$, либо положительно $(k =  + 1)$, либо отрицательно искривленным$(k =  - 1)$. Эти три возможности лучше понять, рассмотрев две свободно движущиеся частицы, которые в начальный момент времени двигаются  параллельно друг другу. В плоской Вселенной частицы продолжают двигаться параллельно друг другу до тех пор, пока они двигаются свободно. В случае $k =  + 1$ первоначально параллельные траектории частиц пересекутся, как линии постоянной долготы пересекаются на Северном и Южном полюсах. Наконец, во Вселенной с $k =  - 1$первоначально параллельные траектории расходятся, как два шарика, катящиеся по седлу.
Используя известные выражения для компонентов тензора кривизны [1]

(точки означают производные по времени) и выражение для тензора энергии-импульса идеальной жидкости

($\rho $и$p$- плотность энергии и давление всех компонентов, представленных во Вселенной в рассматриваемый момент времени), получим два независимых уравнения, описывающих динамику масштабного фактора (уравнения Фридмана [2])

Заметим, что следствием этих двух уравнений является уравнение

которое, как не трудно увидеть, представляет первый закон термодинамики для идеальной жидкости с постоянной энтропией $(dS = 0)$

$k = 0$ (в нашу эпоху и всегда, т.к.  $k = const$), если текущая плотность энергии во Вселенной

где ${H_0}$- текущее значение параметра Хаббла $H$, называемое постоянной Хаббла. В дальнейшем мы будем всегда использовать нижний индекс «0» для значения любой характеристики в настоящее время.
Введем понятие относительной плотности $i$-ого компонента плотности энергии:

Одна из полезных особенностей такой параметризации прямая связь между материальным содержанием Вселенной и ее геометрией. В терминах $\Omega $ первое из уравнений Фридмана (5) запишется в виде

Чтобы решить уравнения Фридмана, надо определить содержание материи во Вселенной и построить уравнение состояния для каждого компонента. В простейшей, линейной параметризации уравнение состояния имеет вид

Решая уравнения Фридмана для случая $w = const$, $k = 0$ получим

(Мы нормируем масштабный фактор условием $a\left( {{t_0}} \right) = 1$.) Эти решения имеют место только в случае $w \ne  - 1$. Последний случай мы рассмотрим особо. Для Вселенной, в которой доминирует излучение (релятивистский газ фотонов и нейтрино) $w = 1/3$, в то время как в случае доминирования материи $w = 0$. Как следствие таких уравнений состояния, для случая материи получим

Последний результат можно понять как простое следствие сохранения числа частиц.  Для излучения

Этот результат является следствием того, что плотность энергии излучения убывает как ${a^{ - 3}}$за счет увеличения объема (расширение Вселенной) и как ${a^{ - 1}}$ ? за счет красного смещения. Заметим, что из уравнения (6) следует, что $\rho  = {\mathop{\rm co}\nolimits} nst$ для \[w =  - 1\]. В этом случае скорость Хаббла остается постоянной, приводя к экспоненциальному росту масштабного фактора

Таким образом, в случае традиционных космологических компонентов – материя и излучение $(w = 0,w = 1/3)$расширение Вселенной может только замедляться, $\ddot a < 0$.
Сделаем небольшое историческое отступление. Первые представления об устройстве Вселенной появились одновременно с мыслящим человеком. Тем не менее основной объем космологических знаний был собран в ХХ веке, называемом золотым веком космологии. Интенсивность исследований особенно увеличилась в последнее время. Чтобы понять темпы накопления данных, используем только один пример. В 1985 году мы знали положения примерно 1100 галактик, теперь более полумиллиона.
Успех обязан двум причинам. С одной стороны, общая теория относительности Эйнштейна позволила перейти от наивных спекуляций о строении Вселенной к строгим физическим моделям. С другой стороны, появление все более и более мощных телескопов, действующих в различных участках спектра электромагнитных волн, позволило существенно расширить масштаб космологических наблюдений и тем самым надежнее установить адекватность используемых моделей. К концу века сложилось впечатление, что мы не только владеем пониманием основ строения Вселенной, но можем достаточно точно предсказывать удаленные этапы ее эволюции.
Так, например, авторы обзора [3] смело утверждали: «С нашим текущим пониманием физики и астрофизики многие вопросы конечной судьбы Вселенной могут быть качественно решены. Наша цель продолжить развитие качественной теории будущего». Авторы обзора проследили десятки этапов эволюции Вселенной вплоть до фантастических времен $ \sim {10^{100 - 200}}$ лет. Созданная ими классификация по точности намного превзошла описанную Г. Аверченко: «История мидян темна и неизвестна, ученые делят ее тем не менее на три периода». Такая благостная ситуация резко изменилась в конце 90-х годов, когда две независимые группы объявили об открытии ускоренного расширения Вселенной [4,5]. Это открытие полностью изменило представление о том, из чего устроена Вселенная, и рано или поздно изменит всю физику в целом.
Почему это открытие является принципиальным? Как видно из второго уравнения Фридмана (5), до тех пор пока $\left( {\rho  + 3p} \right) > 0$ гравитация является притягивающей, и ускоренное расширение Вселенной ($\ddot a > 0$) невозможно. Необходимо введение новой сущности с отрицательным давлением – темной энергии:ускоренное расширение Вселенной возможно при наличии компонента с $w <  - 1/3$. Существование такого компонента кажется в настоящее время практически неизбежным. В большинстве адекватных космологических моделей он обеспечивает основную часть плотности энергии. Будучи концептуально достаточно «простым» (энергией вакуума), он бросает вызов здравому смыслу. Энергия этого компонента растет по мере его адиабатического расширения: энергия системы увеличивается за счет работы, выполненной над системой отрицательным давлением. Такое поведение находится в разительном контрасте с тем, что было бы для любого компонента с положительным или нулевым давлением. Именно этот компонент должен определить дальнейшую судьбу Вселенной.
Второе важнейшее открытие [4,5], сделанное в это же время, состоит в том, что наша Вселенная является плоской (евклидовой, $k = 0$), или, другими словами, мы живем во Вселенной с критической плотностью

Значение ${\Omega _{tot}} \simeq 1$ подтверждено целым рядом наблюдений. Этот результат не явился столь неожиданным, как обнаружение ускоренного расширения Вселенной. Он был предсказан теорией инфляции, созданной в 80-е годы прошлого века, см. [6]. Инфляция ? экстремально простая идея, базирующаяся на доминировании в ранней Вселенной вакуумной плотности энергии, связанной с гипотетическим скалярным полем, называемым инфлатоном. Его природа неизвестна. Является это поле фундаментальным, композитным или чем-то промежуточным. Однако всегда можно использовать эффективное описание в терминах скалярного поля с эффективным потенциалом, управляющим расширением Вселенной.
Этот основной сценарий породил несколько конкретных фундаментальных предсказаний: плоская Вселенная с почти масштабно-инвариантной адиабатической плотностью возмущений с гауссовыми начальными условиями. Инфляция объясняет, почему наш локальный клочок Вселенной является пространственно плоским, т.е. эвклидовым. Такое геометрическое свойство нестабильно относительно эволюционных уравнений теории Большого Взрыва в присутствие материи и излучения. Это делает очень мало вероятным приготовление Вселенной с такими специфическими начальными условиями, если бы не некоторые инфляционные механизмы на ранней стадии эволюции Вселенной. Приближенное постоянство плотности энергии обеспечиваем чудовищное расширение Вселенной. Поэтому первоначально искривленное трехмерное пространство быстро станет неотличимым от плоского гиперпространства.
Подчеркнем не совсем удачный термин – плоский. Очевидно, что Вселенная не двумерна плоска, а трехмерно эвклидова. Этот же механизм объясняет, почему мы не видим ряби, т.е. больших неоднородностей в пространственно-временных структурах, например, больших анизотропий в температурном поле реликтового излучения, когда смотрим в разных направлениях. Гигантское растяжение в процессе инфляции сглаживает любую первичную неоднородность.
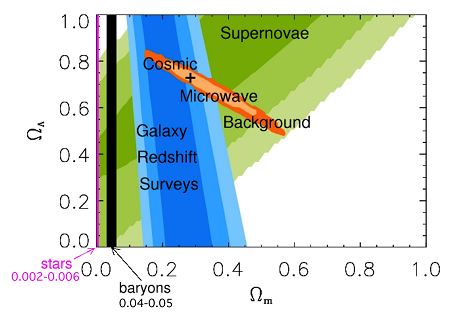
Из чего может быть построена $\Omega  = 1$, так чтобы удовлетворить всему набору имеющихся наблюдений? В настоящее время наблюдения вспышек сверхновых, микроволнового космического фона (МКФ) и динамики образования крупномасштабных обеспечили ряд строгих условий на ${\Omega _m}$и${\Omega _{DE}}$ плотность материи и плотность темной энергии (в единицах критической плотности). Эти результаты согласуются между собой и обеспечивают$\left( {{\Omega _m},{\Omega _{DE}}} \right) \approx \left( {0.3,0.7} \right)$, как показано на рис.1. Количество материи в форме барионов (как светящихся, так и темных) также ограничено наблюдениями микроволнового космического фона и относительной распространенностью легких элементов вместе с теорией ядерного синтеза в рамках  теории Большого Взрыва. Эти данные, рассмотренные совместно, оказываются впечатляюще согласованными, обеспечивая второй эшелон поддержки текущей Стандартной космологической модели. Если объединить все эти наблюдения, то плотность энергии небарионной темной материи (происхождение термина «темная материя» станет понятно ниже), барионов, темной энергии и излучения такова:

В центре нашего внимания будет компонент ${\Omega _{DM}}$- темная материя. Полная программа исследования темной материи должна ответить на следующие вопросы:
$ \bullet $Какие частицы образуют темную материю?
$ \bullet $Темная материя состоит из одного компонента или нескольких?
$ \bullet $Каковы квантовые числа частиц, из которых состоит темная материя?
$ \bullet $Каково взаимодействие этих частиц?
$ \bullet $Как и когда они возникли?
$ \bullet $Почему плотность ${\Omega _{DM}}$имеет наблюдаемое значение?
$ \bullet $Как темная материя распределена в настоящее время?
$ \bullet $Какова ее роль в образовании структур?
$ \bullet $Абсолютно ли стабильна темная материя?
Конечно, для ответа на все эти вопросы надо начать с проблемы детектирования темной материи. Когда мы говорим о проблеме детектирования темной материи, то этот вопрос следует разделить на две большие части:
1. Проблема детектирования темной материи как таковой, т.е. в целом. Эта проблема решается детектированием особенностей динамики крупномасштабных структур. Начало этим исследованиям было положено еще в 30-е годы.
2. Проблема детектирования частиц, из которых состоит темная материя. Это принципиально другая задача. Еe решает не космология, а физика элементарных частиц.
Наличие этих двух различных по своей природе проблем, говорит о том, что ни космология, ни физика элементарных частиц не могут в отдельности решить проблему темной материи. Разумеется, прежде чем перейти к проблеме детектирования, нам следует обсудить предполагаемые свойства объекта, который мы собираемся детектировать.
Завершим введение следующим замечанием. Любая «новаторская» деятельность в космологии может быть интерпретирована в терминах модификации либо левой, либо правой части  уравнений Эйнштейна (1). То есть, если представлять Вселенную как космический автомобиль, то у нас есть две возможности улучшить характеристики автомобиля: либо залить новое топливо в бак (включить новые элементы в тензор энергии-импульса), либо изменить конструкцию автомобиля (модифицировать общую теорию относительности). Какой путь является более перспективным? Для ответа на этот вопрос обратимся к истории физики. Со времен Ньютона движения астрофизических объектов описываются в рамках закона всемирного тяготения. При этом любые отклонения наблюдаемых движений от ожидаемых траекторий способствовали более глубокому пониманию Вселенной.
В частности, всякий раз, когда в движении планет солнечной системы возникали аномалии, возникал естественный вопрос: следует трактовать такие аномалии как опровержение законов гравитации или как указание на существования невидимых (согласно нынешней терминологии «темных») объектов? Классический пример: аномалии в движении Урана привели к догадке о существовании Нептуна, открытого значительно позже. Обратный пример: попытки объяснить аномалии в движении Меркурия существованием новой планеты, названной Вулканом, оказались непродуктивными, и правильное решение было найдено в рамках общей теории относительности, т.е. с помощью введения более совершенных законов гравитации. Основное внимание в настоящем обзоре будет уделено попыткам решения проблемы с помощью введения новой сущности – темной материи, хотя кратко мы остановимся и на альтернативных возможностях, связанных с модификацией общей теории относительности на больших масштабах.

Эта статья любезно предоставлена нам нашим научным руководителем Болотиным Ю.Л.

Читать продолжение

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.