Каждый физик знаком с тяжелым чувством, следующим за обнаружением фатальной ошибки в красивой теории, придуманной несколько дней назад. Увы, такова судьба большинства красивых теорий. Не обошла она и теорию инфляции. Как обычно, дьявол таился в деталях. При более внимательном анализе выяснилось, что ложный вакуум распадается не так гладко, как ожидалось. Эта заметка является продолжением статьи Космическая инфляция: ненавязчивое введение

Процесс распада вакуума похож на кипение воды. Посреди ложного вакуума случайным образом появляются маленькие пузырьки вакуума истинного (рис. 6.1). Внутренние области растущих пузырьков остаются пустыми, а вся энергия, выделяющаяся при переходе ложного вакуума в истинный, сконцентрирована в расширяющихся стенках пузырьков. Когда пузырьки сталкиваются и сливаются, их стенки распадаются на элементарные частицы. Конечным результатом становится истинный вакуум, заполненный плотной горячей материей.

Именно так происходит, если пузырьки возникают в бешеном темпе и весь процесс распада завершается меньше чем за один период удвоения. Это означает, однако, что инфляция заканчивается слишком быстро, намного раньше, чем вселенная становится однородной и плоской. Нас же интересует противоположный случай, когда темп формирования пузырьков низкий, так что вселенная может расшириться во много раз, прежде чем пузыри начнут сталкиваться. Но, как любил говорить швейцарский физик Пауль Эренфест, здесь-то лягушка и прыгает в воду.

Трудность состоит в том, что пространство между пузырьками заполнено ложным вакуумом, а значит, быстро расширяется. узырьки растут очень быстро, со скоростью, близкой к скорости света, но это не сравнится с экспоненциальным расширением ложного вакуума. Если пузырьки не столкнутся в течение одного периода удвоения от момента возникновения, то в дальнейшем расстояние между ними будет только расти, так что они уже никогда не столкнутся.

Выходит, инфляция может никогда не закончиться. Пузыри неограниченно растут в размерах, а в промежутках между ними все продолжают появляться новые. В результате замечательная однородность, порожденная инфляцией, полностью разрушается. Отсутствие подходящего финала для инфляционного расширения стали называть проблемой изящного выхода.

Гут осознал эту проблему спустя несколько месяцев после того, как представил свою новую теорию публике. К тому времени его статья об инфляции еще не была написана, причем по очень простой причине: Алан Гут — самый большой в мире любитель откладывать дела на потом. (Я убедился в этом лично, работая с ним в ряде исследовательских проектов.) Он, конечно, был разочарован, обнаружив в теории серьезный прокол, однако продолжал считать, что идея слишком удачна, чтобы быть ошибочной. Дописав наконец к августу 1980 года свою статью, Гут закончил ее словами: "Я публикую эту статью в надежде, что она... побудит других найти способ обойти нежелательные особенности инфляционного сценария".

Скалярное поле

Чтобы разобраться в истоках проблемы, давайте подробнее обсудим ложный вакуум. Процесс его распада был изучен гарвардским физиком Сиднеем Коулманом (Sidney Coleman), который описал его в терминах так называемых скалярных полей.

Поле — это количественная характеристика, имеющая определенное значение в каждой точке пространства. Его значения могут меняться от точки к точке, а также во времени. Простым примером поля является температура. Северный полюс, мыс Кейп-Код, центр Солнца — все это точки Вселенной, имеющие определенную температуру. Другой знакомый пример — магнитное поле. В дополнение к величине оно обладает также и направлением. Мы не ощущаем магнитного поля, но его присутствие обнаруживается, если взглянуть на компас. Стрелка указывает направление поля, а его напряженность можно определить по тому, насколько сильно оно действует на стрелку, заставляя принять это направление.

Поля, подобно температуре не имеющие направления, называются скалярными. Они описываются одним числом: величиной. Скалярные поля играют важную роль в физике элементарных частиц. Согласно современным теориям, пространство Вселенной заполнено рядом скалярных полей, величины которых определяют энергию вакуума, а также массы частиц и их взаимодействия. Другими словами, эти поля задают вакуум, в котором мы живем. В настоящее время значения скалярных полей соответствуют истинному вакууму, но в прошлом они могли быть иными.

Чтобы проиллюстрировать физику распада вакуума, рассмотрим единственное скалярное поле и сконцентрируемся на том, как оно влияет на энергию вакуума. Каждый кубический сантиметр пространства содержит энергию, которая зависит от величины поля. Точный характер зависимости пока неизвестен, однако в общих чертах он напоминает холмистый ландшафт, как на рисунке 6.2, с максимумами на одних значениях и минимумами на других. Поведение скалярного поля очень похоже на поведение шарика, катящегося по поверхности с рельефом, подобным этому энергетическому ландшафту. В зависимости от начального положения шарик скатится в тот или иной энергетический минимум. Самый нижний минимум имеет почти нулевую плотность энергии; он отвечает истинному вакууму. Более высокий минимум соответствует высокоэнергичному ложному вакууму.

Допустим, мы начинаем с ложного вакуума во всех точках пространства. Это соответствует шарику, покоящемуся в верхнем минимуме. Он будет лежать там очень долго, пока что-нибудь не подтолкнет его вверх, сообщив энергию, необходимую для того, чтобы преодолеть барьер и попасть в нижний минимум. Однако, согласно квантовой теории, объект может "туннелировать" сквозь энергетический барьер. Когда вы наблюдаете такое событие, то видите, как шарик исчезает и мгновенно материализуется по другую сторону барьера.

Квантовое туннелирование — вероятностный процесс. Нельзя точно предсказать, когда оно произойдет, но можно вычислить вероятность, с которой оно случится в заданный отрезок времени. Для макроскопических объектов вроде шарика вероятность туннелирования чрезвычайно мала. Если, к примеру, вы хотите, чтобы банка колы туннелировала к вам из торгового автомата, время ожидания намного превысит современный возраст Вселенной. Однако в микроскопическом мире элементарных частиц квантовое туннелирование распространено гораздо шире.

В случае ложного вакуума вероятность того, что большая область пространства туннелирует в состояние истинного вакуума, совершенно ничтожна. Туннелирование происходит в крошечных, микроскопических областях, приводя к появлению маленьких участков истинного вакуума. Это и есть процесс образования пузырьков, который обсуждался в предыдущей главе. Вероятность туннелирования может быть выше или ниже в зависимости от формы энергетической функции. (Она выше для низких и узких энергетических барьеров.)
Несмотря на сходство между туннелированием шарика и скалярного поля, между ними есть важное различие. Мяч туннелирует между двумя разными точками в пространстве, тогда как скалярное поле — между различными значениями поля в одном и том же месте.

Из нашего анализа следует, что, если между двумя вакуумами имеется энергетический барьер, распад вакуума может происходить только через квантовое туннелирование. Его результатом становятся случайным образом разбросанные пузырьки, которые никогда не сливаются, так что процесс распада никогда не завершается. Но что случится, если мы удалим барьер?

Тише едешь — дальше будешь

Молодой российский космолог Андрей Линде был первым, кто рассмотрел не общепринятые модели скалярного поля без барьера между истинным и ложным вакуумами.

Как и прежде, предположим, что все начинается с маленькой замкнутой вселенной и скалярного поля в состоянии ложного вакуума. Если барьера нет, шарик, представляющий попе, просто скатывается вниз в сторону истинного вакуума (рис. 6.3). Нет никаких пузырьков, а поле, катясь вниз, остается однородным во всем пространстве. Достигнув нижней точки, оно начинает колебаться вверх и вниз. Энергия этих колебаний быстро рассеивается, порождая огненный шар частиц, а поле успокаивается на минимальной энергии.

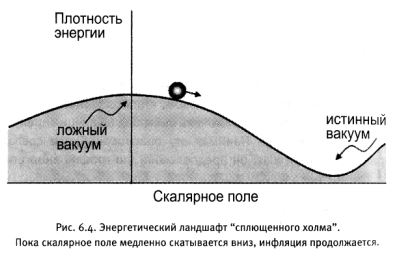
Трудность, однако, состоит в том, что в отсутствие барьера поле будет скатываться вниз очень быстро, и инфляция прекратится слишком рано. Понимая эту опасность, Линде сделал принципиальный шаг: он предположил, что график энергетической функции напоминает по форме холм с очень пологим склоном, как на рисунке 6.4.

Плоский участок наверху холма играет роль ложного вакуума. Если поместить шарик где-то на этом участке, он начнет катиться крайне медленно. При этом он будет оставаться практически на одной и той же высоте, поскольку склон очень пологий. Теперь вспомните, что высота на рисунке соответствует плотности энергии скалярного поля, а ее постоянство — все, что требуется для поддержания неизменно-го темпа инфляции.

Ключевая идея Линде состояла в том, что вблизи вершины холма скалярное поле катится очень медленно, и потому пройдет много времени, прежде чем оно пересечет эту область. Между тем вселенная продолжает расширяться, колоссальным образом вырастая в размерах.

Попав на крутую часть энергетического склона, поле начинает катиться быстрее, а достигнув наконец минимума, осциллирует и расходует свою энергию на порождение горячей смеси частиц. В этот момент мы получаем горячую расширяющуюся вселенную, которая к тому же является однородной и почти плоской. Проблема изящного выхода решена!

Все, что нужно, — это скалярное поле, энергетическая функция которого имеет функцию приплюснутого холма, как на рисунке 6.4. Вы может спросить: а как скалярное поле в самом начале оказалось на вершине холма? Хороший вопрос. Однако отложим его до на другой раз.

Статья Линде появилась в феврале 1982 года, и ту же по сути идею независимо опубликовали американские физики Анд-реас Олбрехт (Andreas Albrecht) и Пол Стейнхардт (Paul Steinhardt). Теория инфляции была спасена.

Другой важный вопрос — действительно ли подобное скалярное поле существует в природе. К сожалению, этого мы не знаем. Нет никаких прямых свидетельств его существования. Скалярные поля, появляющиеся в простейших теориях электрослабого взаимодействия и Великого объединения, обладают энергетическими функциями, слишком крутыми для инфляционной теории.

Однако существует класс так называемых супер-симметричныхтеорий, включающих множество скалярных полей с плоской энергетической функцией. Теория суперструн, которая на сегодня является основным кандидатом на роль самой фундаментальной теории природы, принадлежит как раз к этому классу.

Отрывок из книги А. Виленкина "Many Worlds in One: The Search for Other Universes"

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.