Квантовое описание гравитационного взаимодействия до сих пор не осуществлено вполне удовлетворительным образом. Вместе с тем, квантовая природа всех прочих взаимодействий, по-видимому, этого требует.

Квантовая теория гравитации, возможно, позволила бы решить важнейшие физические проблемы, такие как проблема космологической сингулярности и проблема микроструктуры пространства - времени. Первая из этих проблем не так давно была предметом довольно подробного обсуждения в литературе. Для ее решения привлекался подход Уилера - де Витта [1-3], представляющий собой каноническое квантование гравитации в переменных метрического тензора. Согласно этому подходу, вселенная в целом описывается волновой функцией, подчиняющейся ряду уравнений, главным из которых является уравнение Уилера - де Витта. Однако указанный подход порождает новые вопросы и проблемы, не менее серьёзные, чем классическая проблема космологической сингулярности, которую таким образом пытались решить. Так, волновая функция вселенной подразумевает вероятностное описание ее свойств. Но наша Вселенная существует в единственном экземпляре и неясно, как такое описание может в принципе возникнуть. Другая проблема связана с тем фактом, что волновая функция вселенной не зависит от времени как такового, и возникает вопрос, каким образом такая волновая функция в принципе может описывать Вселенную, которая эволюционирует во времени.

Вопрос о микроструктуре пространства - времени гораздо реже обсуждается в литературе. Настоящая работа посвящена этому вопросу, а также связанному с ним вопросу о спонтанном квантовом рождении новой вселенной и оценке вероятности такого процесса. При описании микроструктуры пространства - времени часто употребляют введённый Уилером термин "пространственно-временная пена", подчёркивающий ее квантовую природу. Действительно, если придерживаться обычных представлений квантовой теории поля, то нужно согласиться, что на достаточно малых пространственно-временных масштабах становится существенной квантовая природа метрики пространства-времени, и что нельзя говорить о ее определённом классическом значении. Достаточно полное описание этой "пены" представляет очень сложную задачу. Мы ограничимся рассмотрением некоторого нового класса конфигураций геометрии, которые естественно назвать квазизамкнутыми мирами [4-6].

Рассмотрим пространственную конфигурацию, подобную изображённой на рис. 1, а. Большое по своим размерам трёхмерное Риманово пространство $M$ соединено небольшой горловиной с малым пространством $N$, которое, ввиду малости метрического размера горловины, мы можем назвать полузамкнутым миром. При классической эволюции такой трёхмерной конфигурации во времени полузамкнутый мир с точки зрения большого мира приближенно выглядит как некая "частица" с массой, вообще говоря, тем меньшей, чем меньше размер горловины.

Мы можем предположить, что подобные конфигурации возникают в результате вакуумных квантовых флуктуации метрики и существуют тем дольше, чем меньше их масса (или,что то же, их внутренняя энергия). Тем самым такие долгоживущие конфигурации с малой массой естественно выделяются на фоне всевозможных флуктуаций геометрии [5]. Их спонтанное образование можно интерпретировать как квантово-гравитационную неустойчивость однородного вакуума.

В предельном случае нулевого размера горловины, изображённой на рис. 1, а, малый полузамкнутый мир как бы замыкается полностью, но мы не исключаем возможности того, что он остаётся прикреплённым к материнскому миру. Соответствующая конфигурация изображена на рис. 1, б. Здесь два замкнутых мира, большой и малый, соединяются в точке а. Практически это означает, что мы отождествляем соответствующие точки в этих пространствах.

Несколько отвлекаясь, мы отметим, что наличие квантовых флуктуаций геометрии, вообще говоря, не исключает возможности упорядоченной структуры основного состояния (вакуума). Если предположить, как это сделано в работах одного из авторов [4. 5]э что эта структура имеет форму "кристалла", роль "атомов" которого играют долгоживущие флуктуации указанного типа (рис. 2), то это позволило бы решить ряд важных проблем квантовой теории поля, таких как проблема расходимостей и проблема космологической постоянной, и объяснить дублирование фермионных поколений элементарных частиц. Од-нако в настоящей работе эти вопросы затрагиваться не будут; здесь мы строим теорию лишь одного из возможный таких "атомов", представляющего собой конфигурацию типа изображенной на рис. 1, б или рис. 2.

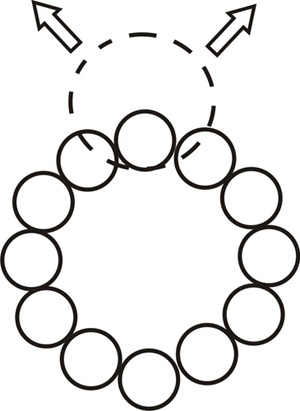
Рис. 2

В следующей части работы, ограничиваясь рамками минисуперпространства, вычислим вероятность туннелирования микровселенной в область больших ее размеров и, тем самым, рождения из нее новой вселенной [7, 8]. Предполагаем, что такого рода событие будет каким-то образом сказываться в большом мире, но в этой работе не уточняем его возможные последствия.

Вероятность туннелирования микровселенной.

Минисуперпространственная модель квазизамкнутого мира описывается фридмановской метрикой вида

\begin{equation} ds^2 = c^2dt^2-a^2(t)d\Omega,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (1) \end{equation}

где $d\Omega$ - метрика трёхмерной сферы единичного радиуса и с - скорость света. Квазизамкнутый мир "приклеен" к большой материнской вселенной, как это изображено на рис. 1, а, и движется в ней вдоль некоторой времениподобной мировой линии. При этом параметр $t$ отсчитывает собственное время вдоль этой мировой линии, а переменная $a(t)$ описывает внутреннюю динамику (размер) квазизамкнутого мира. Заметим, что отсутствие обычной функции хода $N(t)$ в качестве множителя при $dt^2$ в выражении (1) объясняется тем, что в нашей теории время t есть внешнее (с точки зрения микровселенной) измеряемое время, а не просто внутреннее время квазизамкнутого мира. В связи с этим полная энергия квазизамкнутого микромира будет в нашей теории отлична от нуля, по сравнению с обычной теорией замкнутого мира. Подробная и последовательная формулировка теории квазизамкнутого мира будет обсуждаться в нашей расширенной публикации. Действие Гильберта - Эйнштейна с учётом возможного $\Lambda$-члена есть

\begin{equation} S = -\frac{c^3}{16\pi G_N} \int\left(R+2\Lambda\right)\sqrt{-g}d^4x,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (2) \end{equation}

где $G_N$ - ньютоновская гравитационная постоянная. Для метрик вида (1) это действие принимает вид

\begin{equation} S = -\frac{3\pi c^4}{4 G_N}\int\left(\frac{\dot{a}^2a}{c^2}-a+\frac{\Lambda}{3}a^3\right)dt, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (3) \end{equation}

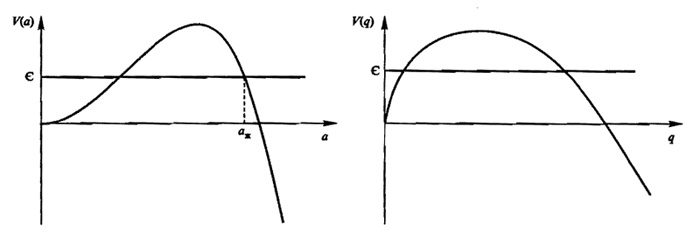
Рис. 3

Классическжй потенциал $V(a) \propto a^2-\Lambda а^4/3$, соответствующий действию (3), приведен на рис. 3(слева). В действии удобно произвести замену переменной $q = \left(\sqrt{\pi}a/l_P\right)$, времени $\tau=3\sqrt{\pi}t/4t_P$ и космологической постоянной $\lambda=l_P^2\Lambda/3\pi$, где $l_P=\sqrt{ \hbar G_N/c^3} \approx1.6 \cdotp 10^{-33}cm$ есть планковская длина, а $t_P=l_P/c\approx 5.4\cdotp 10^{-44}c$ - планковское время. Тогда действие (3) примет вид

\begin{equation} S = -\hbar \int\left(\frac{1}{4}\dot{q}^2-q^{2/3}+\lambda q^2\right)d\tau,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (4) \end{equation}

Соответствующий классический потенциал $V(q)$ в терминах переменной $q$ приведен на рис. 3(справа).

Волновая функция $\psi (\tau,\,q)$ квазизамкнутого мира, движущегося вдоль некоторой мировой линии большого материнского мира, удовлетворяет уравнению Шрёдингера

\begin{equation} i\hbar\frac{\partial\psi (\tau,\,q) }{\partial \tau}=\hat{H}\psi (\tau,\,q). \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (5)\end{equation}

Согласно действию (4), уравнение (5) принимает вид

\begin{equation} i\hbar\frac{\partial\psi (\tau,\,q) }{\partial \tau}=\left[\frac{\partial ^2}{\partial q^2}-q^{2/3} +\lambda q^2\right]\psi (\tau,\,q), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (6)\end{equation}

Граничные условия, при которых оператор в уравнении (6) самосопряжён, суть $\psi(0)=0$ или $\psi '(0)=0$. Для получения конкретных решений уравнения (6) необходимо задать начальные условия на волновую функцию во времени т, а также граничное условие в пространстве параметра $q$ при $q=0$. Граничное условие при $q = 0$ определяется условием сохранения полной вероятности, т.е. условием самосопряженности оператора $\hat{H}$. В качестве начального условия мы положим, что волновая функция при некотором начальном времени $\tau$ локализована в области локального минимума $q = 0$ потенциала гамильтониана. Тогда задача, описываемая уравнением (6), формально совпадает с задачей о квазистационарных состояниях и туннелировании в область больших значений $q$ в потенциале $V(q)=q^{2/3}-\lambda q^2$ (см. рис. 4). Теория решения такой задачи (теория Гамова) довольно хорошо разработана (см. [11]), и мы применим ее для рассматриваемого случая.

Как известно [11], чтобы получить вероятность туннелирования в задаче (6), необходимо найти формальные стационарные решения уравнения (6) и соответствующие им комплексные уровни энергии е с граничным условием: при $q\rightarrow \infty$ волновая функция $\psi (\tau,\,q)$ имеет вид уходящей волны.

Таким образом, необходимо решить уравнение

\begin{equation} \left[\frac{d^2}{dq^2}-q^{2/3}+\lambda q^2\right]\psi =\epsilon\psi. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (7) \end{equation}

Его комплексные уровни имеют вид $\epsilon =\epsilon_0 - i\gamma/2,$ где $\epsilon_0$ и $\gamma$ - вещественны и положительны. При этом среднее собственное время жизни соответствующего квазистационарного состояния равно $t_*\sim t_P/\gamma$.

Сделаем оценку для энергии нижайших уровней. Если параметр $\lambda$ мал, то мы можем рассматривать слагаемое $\lambda q^2$ как возмущение. Тогда в первом порядке по $\lambda$ получаем, что нижайший уровень \begin{equation} \epsilon_0 \sim 1.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (8) \end{equation}

Теперь оценим мнимую части энергии. С экспоненциальной точностью имеем (см. [11])

\begin{equation} \gamma\sim\exp\left[-2\int\limits_{q1}^{q2} {\sqrt{q^{2/3}-\lambda q^2 -\epsilon_0}}dq\right], \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (9)\end{equation}

где $q1$ и $q2$ - корни подынтегрального выражения. В случае, когда параметр $\lambda\ll1$, мы получаем асимптотическое выражение

\begin{equation} \gamma\sim e^{-1/\lambda+3\pi\epsilon_0/4\sqrt{\lambda}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (10) \end{equation}

и соответствующее собственное время жизни

\begin{equation} t_*\sim t_P e^{-1/\lambda+3\pi\epsilon_0/4\sqrt{\lambda}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (11) \end{equation}

Полученными выше формулами можно пользоваться в первом приближении и в случае, когда космологическая "постоянная" достаточно медленно (адиабатически) меняется со временем $t$. Адиабатичность означает, что вероятность возбуждения квазизамкнутого мира (т.е. вероятность его перехода на возбуждённый квазидискретный уровень) мала. Подобная ситуация имеет место, например, в ситуации космологического раздувания большого мира (см. [12]), когда эффективная космологическая постоянная зависит от значения потенциала некоторого скалярного поля ф вдоль мировой линии движения квазизамкнутого мира и медленно убывает со временем. В случае, когда космологическая постоянная в микромире целиком генерируется за счёт этого скалярного поля, формула (11) выражает текущее (на данный космологический момент) время жизни квазизамкнутого мира. Легко показать, что в рассматриваемых условиях время жизни квазизамкнутой микровселенной в одном из нижайших квазистационарных уровней больше времени расширения большой вселенной. Действительно, оценим значение космологической постоянной, при котором время жизни (11) совпадает с хаббловским временем $t_H$ расширения большой вселенной в условиях, когда космологическая постоянная доминирует в плотности энергии. Мы имеем ($H$ есть хаббловский параметр большой вселенной):

\begin{equation} H^2=c^2\Lambda/3=\pi\lambda/t_P^2,\,\,\,\,\,\,t_H\equiv H^{-1}=t_P/\sqrt{\pi\lambda},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (12) \end{equation}

и условие $t_*\sim t_H$ даёт \begin{equation} \lambda\sim e^{-2/\lambda},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (13) \end{equation} т.е. $\lambda\sim 1,$ или $\Lambda\sim l_P^{-2},$ что имеет место лишь в планковскую эпоху, когда вообще нельзя говорить о классической большой вселенной (состояние мира в эту эпоху существенно квантовое). С течением времени космологическая постоянная убывает, и время жизни (11) экспоненциально возрастает. В настоящую эпоху мы имеем $\lambda\sim 10^{-122},$ и время жизни (11) квазизамкнутых миров практически бесконечно.

Однако микровселенная может обладать своей собственной внутренней космологической постоянной $\Lambda$, которая не обязана совпадать с (эффективной) космологической постоянной большого материнского мира и также не обязана быть малой. В этом случае время жизни (11) зависит от этой космологической постоянной микромира как от (неизвестного) свободного параметра.

В заключение отметим следующее. В каноническом подходе к квантованию гравитации имеются серьёзные и до сих пор не преодолённые трудности, связанные с интерпретацией волновой функции вселенной. Проблема состоит в том, что в этом подходе волновая функция вселенной не зависит от времени и призвана описывать единственный в своём роде объект - нашу Вселенную, из-за чего возникают трудности с ее статистической и эволюционной интерпретацией.

В настоящей работе мы применяем теорию квантовой гравитации с некоторой модификацией не ко всей вселенной, а к ее малым частям, которые мы назвали квазизамкнутыми мирами. Квазизамкнутый мир может рассматриваться как один из "атомов", из которых построено пространство-время нашей Вселенной [4, 5]. Таких "атомов", разумеется, должно быть очень много; при этом статистическая интерпретация их волновой функции ничем не отличается от обычной. Это обстоятельство выгодно отличает наш подход от обычных теорий, в которых волновая функция вселенной относится к одному-единственному объекту - нашей Вселенной, не зависит от какого бы то ни было времени и не имеет удовлетворительной интерпретации.

В этой работе мы вычислили вероятность туннелирования квазизамкнутого мира в единицу времени. Эта вероятность получилась экспоненциально малой для значений космологической постоянной, характерных для реального) мира. Мы, таким образом, можем сделать вывод об устойчивости минивселенной по отношению к туннелированию с образованием большой классической вселенной.

Нетрудно выразить полученную вероятность подбарьерного туннелирования квазизамкнутого микромира (микровселенной) и его превращения в быстро расширяющийся макромир через начальный классический размер этого макромира, который равен

\begin{equation} a_*=l_P/\sqrt{\pi\lambda}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (14) \end{equation}

При условии $\lambda\ll$ будем иметь из (10) \begin{equation} \gamma\sim e^{-\pi a^2_*/l_P^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (15) \end{equation}

и для времени жизни микромира по отношению к процессу туннелирования и превращения в "дочерний" микромир

\begin{equation} t_*\sim t_P e^{\pi a^2_*/l_P^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (16) \end{equation}

Выражения (15) и (16) согласуются с оценками, проведёнными ранее в [7, 8].

Оценим вероятность того, что наша Вселенная на современном этапе ее эволюции уже стала Материнской" по крайней мере для одной "дочерней" вселенной, успевшей "отпочковаться" от неё в результате подбарьерного туннелирования. Если оценивать современный размер Вселенной как $l_0\sim 10^{28}$см, а характерный размер долгоживущих квазизамкнутых микромиров, составляющих микроструктуру пространства Вселенной, как $l\sim l_P\sim 10^{-33}$см, то получим, что весь ансамбль таких планковских микромиров содержит их число порядка

\begin{equation} N\sim (l_0/l_P)^3\sim 10^{183}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (17) \end{equation}

Следовательно, за время порядка современного хаббловского времени $H_0^{-1}\sim 10^{17}$с от нашей Вселенной в среднем отпочковалось \begin{equation} N_0\sim N(1-e^{-1/t_*H_0})\sim N/t_*H_0\sim Ne^{-\pi a_*^2/l_P^2}/t_PH_0\sim 10^{244} \cdot e^{-\pi a_*^2/l_P^2}\sim e^{562-\pi a_*^2/l_P^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (18) \end{equation} дочерних вселенных. При вычислении мы предположили, что $N_0\ll N,$ или, следовательно, $\pi a_*^2/l_P^2 =1/\lambda > \ln(t_PH_0)^{-1} = \ln 10^{61}\approx 140.$ Можно, в принципе, поставить вопрос о возможных наблюдательных проявлениях присутствия расширяющихся "дочерних" вселенных "в окрестности" нашей Вселенной, но этот вопрос выходит за рамки данной работы.

 Авторы: П.И. Фомин, Ю.В. Штанов, О.В. Барабаш

Литература

1. Wheeler J. A. Geometrodynamies and the issue of the final state // Relativity, Groups and Topology / Ed. by C. De Witt and B.S. De Witt. - New York: Gordon and Breach, 1964.
2. De Witt B.S. Quantum theory of gravity. I. The canonical theory // Phys. Rev. - 1967. - 160. - P. 1113.
3. Wheeler J.A. Superspace and the nature of quantum geometrodynamies // Batelle Rencontres / Ed. by C. De Witt and J.A. Wheeler. - New York: Benjamin, 1968.
4. Fomin P.I. Zero cosmological constant and Planck scales phenomenology // Proceedings of the Fourth Seminar on Quantum Gravity, May 25-29, Moscow / Ed. by M.A. Markov. - Singapore: World Scientific, 1988. - P. 813.
5. Фомин П.И. О кристаллоподобной структуре физического вакуума на планковских расстояние // Пробл. физ. кинетики и физики тв. тела. - Киев: Наук, думка, 1990. - С. 387-398.
6. Fomin P.I., Kuzmichev V. V. Gravitational fields of massive and massless axial-symmetric quadrupoles in general relativity // Phys. Rev. D. - 1994. - 49, No 4. - P. 1854-1860.
7. Фомин П.И. Гравитационная неустойчивость вакуума и космологическая проблема. - Киев, 1973. -(Препринт / АН Украины. Ин-т теорет. физики; 73-137Р)
8. Фомин П.И. Гравитационная неустойчивость вакуума и космологическая проблема // Докл. АН УССР. Сер. А. - 1975. - № 9. - С. 831-835.
9. Конопяева Н.П., Попов В.Н. Калибровочные пола. - Москва: Атомиздат, 1980. - 240 с,
10. Фейнман Р., Хиббс А. Квантовая механика и интегралы по путям. - Москва: Мир, 1968.
11. Базь А.И., Зельдович Я.Б., Переломов A.M. Рассеяние, реакции и распады в нерелятивистской кван-товой механике. - Москва: Наука, 1971. - 544 с.
12. Линде А.Д. Физика элементарных частиц и инфляционная космология. - Москва: Наука, 1990. - 280 с.

Комментарии (1):

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.